4.9. Focus Search

4.9.1. Focus Modes

The following focus methods are available:

RMS Spot Size	minimal variance of the lateral ray position
Irradiance Variance	highest irradiance variance
Image Sharpness	sharpest edges for the whole image
Image Center Sharpness	sharpest edges in the center region of the image

The methods use all available rays, for better results the scene should have been traced with much rays as possible. The methods are explained in more detail down below.

There are multiple applications for focus search, below you can find method recommendations.

Case 1: Perfect, nearly ideal focal point

• Examples: Focus of an ideal lens. Paraxial illumination of a real lens

• Preferred methods: RMS Spot Size. Irradiance Variance is also suitable, but has worse performance.

Below you can find an example. Both RMS Spot Size and Irradiance Variance find a similar focal position, differing only in 70 µm. Note the different scaling of the images.

Table 4.12 Comparison between “RMS Spot Size” (left) and “Irradiance Variance” (right) in linear (top) and logarithmic lightness values (bottom). Example Double Gauss. Focus search for ray source 0 only. 2 million rays.

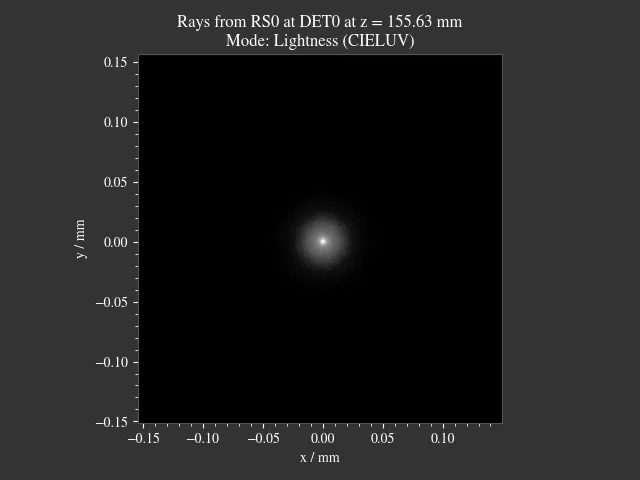
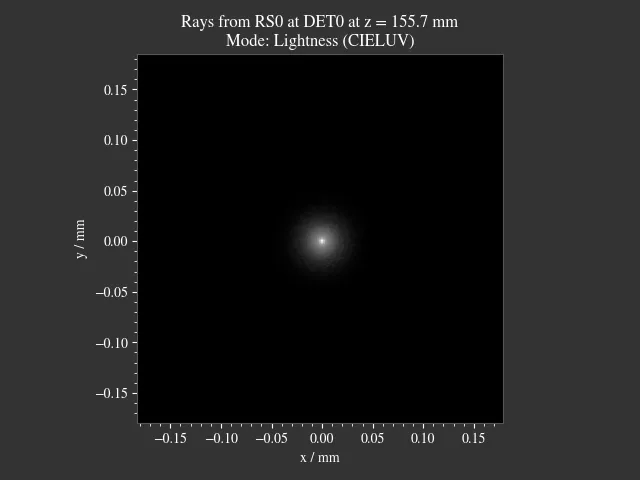
Case 2: Strong aberrations or no distinct focal point

• Examples: Lens with large spherical aberration, multifocal lens

• Preferred methods: Irradiance Variance.

In the following example there are noticeable amounts of spherical aberration. RMS Spot Size tries the minimize the radial distance of the outer rays, sacrificing a sharp core. Irradiance Variance correctly finds a suitable focal position. Note the logarithmic plots, that show the outer rays. In the right case they merely contribute to the image, but they have large impact on the RMS, why the RMS method fails.

Table 4.13 Comparison between “RMS Spot Size” (left) and “Irradiance Variance” (right) in linear (top) and logarithmic lightness values (bottom). Example Spherical Aberration.

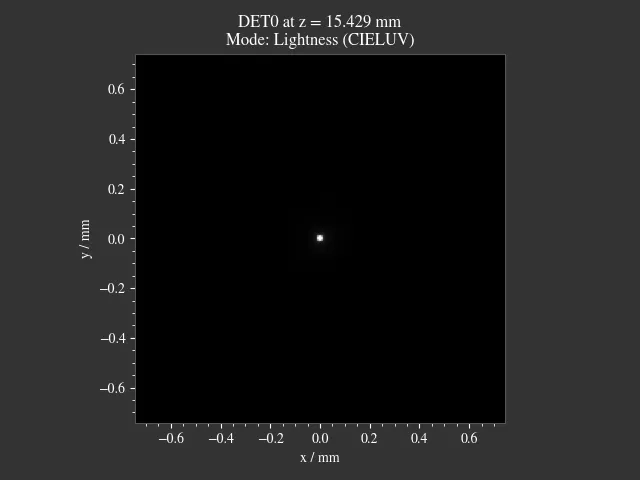
Case 3: Finding the optimal image distance

• Example: Actual image position (not just the paraxial) in a multi-lens setup.

• Preferred methods: Image Sharpness. With large amounts of curvature of field Image Center Sharpness should be selected, to find a best-fit focus for the image center region.

For the image sharpness methods to work best, a source image with high contrast and sharp edges should be used. For instance, the grid or Siemens star presets, depicted in table Table 4.11.

In the following figure you can find an example for image sharpness focussing for a setup with large amounts of field of curvature. While in the left case more image regions are somewhat sharp, in the right case the sharpness is optimized for the center region.

Table 4.14 Comparison between “Image Sharpness” (left) and “Image Center Sharpness” (right) for a setup with large amounts of field of curvature. Example Image Render, Grid image, pupil of 1mm, 5 million rays.

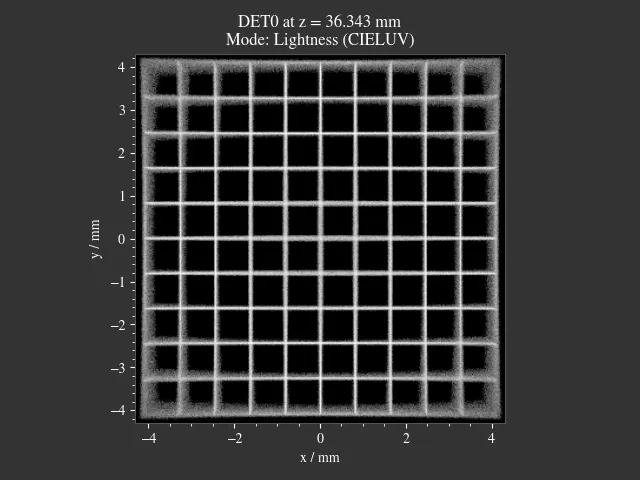
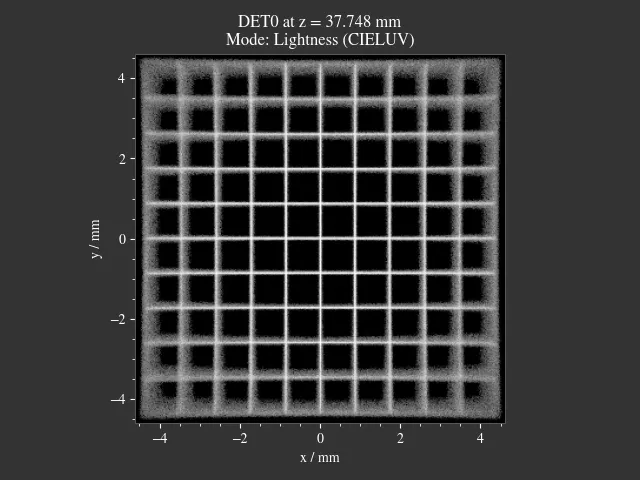
4.9.2. Limitations

Limitations include:

• due to restrictions of the search region the search can’t find a focus that lies between the maximum and minimum z-value of a surface

• rays absorbed in the search region by the raytracer outline are handled as not absorbed

• in more complex cases only a local minimum is found

• see the limitations of each method below.

4.9.3. Usage

For focus search you will need to trace the Raytracer geometry. The focus_search function is then called by passing the focus mode and a starting position. The search takes place around the starting point, with the search region between the largest z-position of the last aperture, filter, lens or ray source and the smallest z-position of the next aperture, filter, lens or outline.

res, fsdict = RT.focus_search("RMS Spot Size", 12.09)

focus_search returns two results, where the first one is a scipy.optimize.OptimizeResult object with information on the root finding. The found z-position is accessed with res.x. The second return value includes some additional information, for instance needed for the cost plot, see Focus Search Cost Function Plots.

By default, rays from all sources are used to focus_search. Optionally a source_index parameter can be provided to limit the search to a specific ray source.

res, fsdict = RT.focus_search("RMS Spot Size", 12.09, source_index=1)

If the output dictionary fsdict should include sampled cost function values, the parameter return_cost must be set to True:

res, fsdict = RT.focus_search("RMS Spot Size", 12.09, return_cost=True)

This is required when plotting the cost function using focus_search_cost_plot, see Focus Search Cost Function Plots. It is deactivated by default to increase the performance of methods "RMS Spot Size", "Irradiance Variance"

4.9.4. Cost Plot

Note

Generally it is recommended to plot the cost function of the optimization so one can see if there are multiple minima and how distinct the found value is. The TraceGUI has an option for plotting the cost function.

See Focus Search Cost Function Plots.

4.9.5. Mathematical Formulations

4.9.5.1. RMS Spot Size

Minimizing the position variance \(\sigma^2\) of lateral ray positions \(x\) and \(y\) at axial position \(z\). All positions are weighted with their power \(P\) when calculating the weighted variance \(\sigma^2_P\). The Pythagorean sum is applied using both variances to get a simple quantity \(R_\text{v}\) for optimization.

(4.22)\[\underset{z \in [z_0, z_1]}{\text{minimize}}~~ R_\text{v}(z) := \sqrt{\sigma^2_{x,P}(z) + \sigma^2_{y,P}(z)}\]

This procedure is simple and performant. However, the disadvantage of this method is that it minimizes the position variance of all beams. For example, if there is a strong outlying halo, the method also tries to keep it as small as possible, which can lead to a compromise between the halo and the size of the actual focus.

4.9.5.2. Irradiance Variance

Renders a two dimensional power histogram \(P(x, y, z)\) for rays at position \(z\). This image is divided by pixel area to get an irradiance image \(E(x, y, z)\). The approach then calculates the variance of the pixel values and finds the \(z\) with the largest variance.

(4.23)\[\underset{z \in [z_0, z_1]}{\text{maximize}}~~ \log{\sigma_E^2(z)}\]

The logarithm is applied for a more compact value range.

The most outside rays define the image dimensions, the absolute image size therefore varies along the beam path. This can be an issue when few rays are far away from the optical axis, since the resolution suffers because of these marginal rays.

The variance is large when there are bright areas in the image (with much power per area) or if there is a large variance between pixels, which should be the case if unblurred structures are present.

4.9.5.3. Image Sharpness

As for the method Irradiance Variance, a power histogram is calculated. The method then maximizes all image gradients, which indicate sharp structures and a high local variance. The magnitude of the gradient is calculated from the Pythagorean sum of its components. Maximizing the sum of all squared magnitudes leads to the following expression:

(4.24)\[\underset{z \in [z_0, z_1]}{\text{maximize}} ~~ \sum_{x, y} \left(\left( \frac{\partial P(x, y, z)}{\partial x}\right)^2 + \left( \frac{\partial P(x, y, z)}{\partial y}\right)^2\right)\]

This is equivalent to:

(4.25)\[\underset{z \in [z_0, z_1]}{\text{maximize}}~~ \sum_{x,y} \left( \frac{\partial P(x, y, z)}{\partial x}\right)^2 + \sum_{x, y} \left( \frac{\partial P(x, y, z)}{\partial y}\right)^2\]

4.9.5.4. Image Center Sharpness

The same procedure is performed as for the Image Sharpness method, but the image is weighted with a rotationally symmetric Hanning window:

(4.26)\[\begin{split}P_w(x, y, z) = P(x, y, z) \cdot \begin{cases} 1 + \cos(\pi r) &~~\text{for}~ r \leq 1\\ 0 & ~~\text{for}~ r > 1\\ \end{cases}\end{split}\]

Here, \(r\) is calculated from the normalized image coordinates \(x, y \in [-1, 1]\).

After weighing the image, its power is normalized. This is done to avoid rewarding images with more light intensity at their center, as the linearity of scaling also leads to higher partial derivatives. This is equivalent to optimizing the ratio of sum of derivatives and image intensities. In the Image Sharpness method this is not required, as the power remains constant in each image, as all rays are included equally.